Trigonometry Review
Table of Contents
- intro about complex numbers
- some properties
- take a vector
- rotate
- derive equation
- derive eulers
- v’ = eitheta v
- give intuition about complex exponentials
In this section, we’ll be reviewing a few trig properties as well as examples of how to derive them. The purpose isn’t to cover them all, but to get you acclimated to the math for the first module.
A handy mnemonic to remember the cosine, sine and tangent relationships in a right triangle is “soh-cah-toa”.
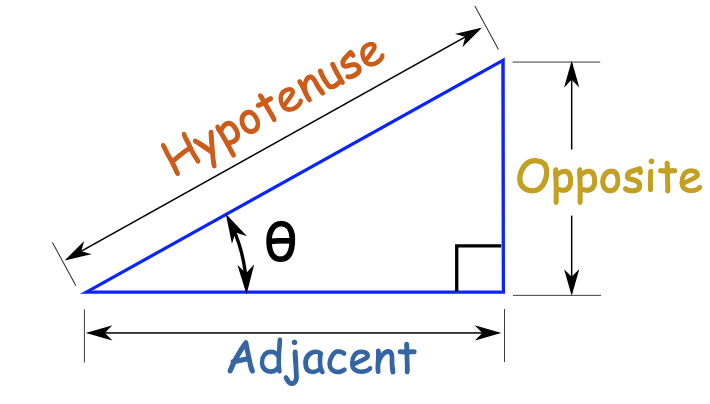
That is, $\sin\theta = \frac{\textbf{o}\text{pposite}}{\textbf{h}\text{ypotenuse}}$, $\cos\theta = \frac{\textbf{a}\text{djacent}}{\textbf{h}\text{ypotenuse}}$ and $\tan\theta = \frac{\textbf{o}\text{pposite}}{\textbf{a}\text{djacent}}$.
We can apply these definitions in a unit circle to derive useful properties of these functions.
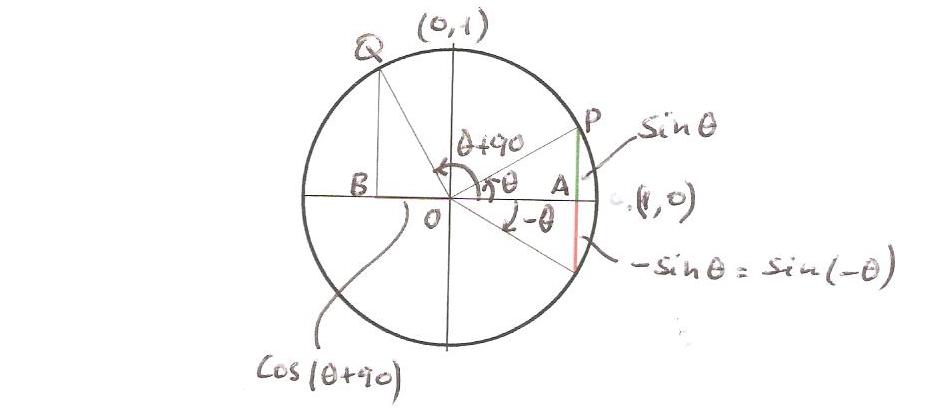
In the figure above, let OP be a radius of the circle with $\angle POA = \theta$. From the definition of sine and cosine, we have that $\cos \theta = OA$ and $\sin \theta = AP$ since $OP = 1$. Thus, the coordinates of the point P are $(\cos \theta, \sin \theta)$. Similarly, we can see that the point drawn at $-\theta$ has the same $x$ value as P but the negative of its $y$ value. This means that we can write an expression relating the cosine/sine of an angle with its negative:
In fact, cosine is an even function and sine is an odd function. Next, consider the point Q, drawn with an angle of $\theta + 90$ from the origin. In the right triangle QPO, the angle Q is equal to $\theta$ and O equal to $90 - \theta$. This means that QBO and OAP are similar triangles. As such,
from which we can derive the expressions for $90 + \theta$:
For more formulas, check out the following cheatsheat.